Le mythe du nombre d’or
Publié en ligne le 30 novembre 2007 - Numérologie et nombre d’or -
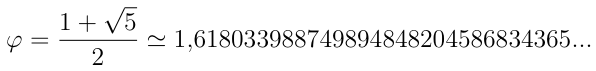
À en croire les nombreux livres et sites Internet qui lui sont dédiés, le nombre d’or, à la fois canon de l’esthétisme et marque divine, serait présent à ce titre depuis la nuit des temps dans beaucoup de constructions humaines ou naturelles 1.

La pyramide de Kheops serait liée au nombre d’or, les dimensions du Parthénon d’Athènes feraient apparaître le nombre d’or. Les gradins du théâtre d’Épidaure, construit en Grèce à la fin du IVe siècle avant JC, seraient répartis grâce au nombre d’or. Des grandes cathédrales européennes, jusqu’au Taj Mahâl, immense monument funéraire élevé en Inde, le nombre d’or ordonnerait les proportions de nombreuses constructions. Ce nombre serait également présent dans les œuvres de Léonard de Vinci, Botticelli, Monet, Degas, Cézanne, mais aussi Dali ou Picasso.
Ce nombre magique et omniprésent ne serait pas uniquement caché dans les œuvres architecturales ou artistiques. On le retrouverait dans la nature elle-même (l’œuvre de Dieu). La « divine proportion » serait celle d’un homme bien proportionné (distance sol/nombril rapportée à la hauteur totale, ou distance sol/nombril rapportée à celle nombril/sommet du crâne) 2. On le retrouverait dans la botanique et la phyllotaxie (étude de la disposition et de l’arrangement des feuilles d’un végétal, et par extension, de tous les arrangements possibles observables chez les végétaux) avec, par exemple, la disposition des spirales dans les fleurs de tournesol ou dans la pomme de pin.
Et pour qui cherche un peu, sur Internet ou ailleurs, il sera aisé de retrouver ce nombre dans de nombreux autres domaines, poésie, littérature, musique, etc.
Qu’en est-il en réalité ? Quelle est la part du mythe, et comment expliquer les faits avérés ?
Une constante mathématique fascinante, comme bien d’autres…
Le nombre d’or est la constante (1+√5)/2, soit environ 1,61803… C’est la racine positive de l’équation du second degré, x2 – x – 1 = 0. Le nombre d’or possède quelques propriétés, conséquences immédiates de sa définition : pour connaître son inverse, il faut lui retrancher 1. Il intervient dans des propriétés du dodécaèdre ou de l’icosaèdre (au même titre que √2 intervient dans le carré, et √3 dans le cube). On le retrouve dans d’autres constructions géométriques (triangle isocèle aux angles de 72°, 72° et 36°, et par conséquent, dans le pentagone régulier, dans les étoiles à 5 branches...).
Le nombre d’or est également lié à la suite de Fibonacci. Celle-ci est présentée de façon récréative par le mathématicien italien Leonardo Pisano (Fibonacci) comme suit : « Possédant initialement un couple de lapins, combien de couples obtient-on en douze mois si chaque couple engendre tous les mois un nouveau couple à compter du second mois de son existence ? ». Le terme de rang n de la suite est égal à la somme des deux termes précédents (sn = sn-1 + sn-2). Pour passer d’un terme au suivant, on multiplie par un nombre qui se rapproche du nombre d’or quand n augmente.
C’est ainsi que l’on parlera tantôt de nombre d’or, de rectangle d’or, de triangle d’or, de section dorée, de spirale d’or, etc. Aucune omniprésence mystérieuse. Toutes ces facettes sont cohérentes, et se déduisent les unes des autres.
Euclide le premier aborde la question du « partage en extrême et moyenne raison » d’un segment AB, c’est-à-dire le point C tel que le rapport de la longueur du segment sur la partie la plus importante soit égal au rapport de cette partie sur la plus petite (AB/AC = AC/CB, voir figure). Ce rapport est équivalent au nombre d’or, dont la valeur algébrique n’a été calculée que bien plus tard.

Contrairement à ce qu’on peut parfois lire, Euclide ne se posait pas la question de savoir « étant donné un segment, comment le partager de façon harmonieuse et plaisante à l’œil » 3. Aucun commentaire esthétique n’accompagnait l’utilisation de ce rapport. D’ailleurs, Euclide ne semble pas avoir accordé plus d’importance à ce rapport qu’à d’autres rencontrés dans son étude de différents polygones. Le nombre d’or n’a en réalité pas une importance hors du commun en mathématiques. Il intervient dans certaines figures géométriques, ainsi que dans des contextes non géométriques. Mais d’autres constantes sont tout aussi importantes : √2, √3, Pi… et tout aussi fascinantes 4.

La Grande Pyramide a été l’objet de nombreuses interprétations cabalistiques. Le chiffre 5 a été largement cité comme une clé dans la construction de l’édifice. Il n’est pas plus difficile de retrouver le chiffre 5 que le nombre d’or dans un monument quelconque, comme l’indique Martin Gardner (voir l’encadré « Les secrets du Washington Monument »).
… que l’on retrouve partout, avec un peu d’effort
Aucun traité d’architecture, de l’Antiquité ou du Moyen Âge, ne mentionne le nombre d’or. Pour l’historien de l’art Rudolph Wittkower, « aussi loin que nous puissions voir, [√2] est le seul nombre irrationnel d’importance impliqué dans la théorie architecturale des proportions à la Renaissance » 5. S’il devait être retrouvé dans une construction, ce serait donc, soit par pur hasard, soit en faisant l’hypothèse d’un savoir secret transmis hors de tout support écrit.
Concernant la pyramide de Kheops, pour trouver le nombre d’or, il faut diviser l’apothème (distance du sommet au milieu d’un des côtés au sol), par la demi-base de la pyramide. Jean-Pierre Adam 6 montre qu’une recherche approfondie dans les dimensions de la guérite de la marchande de billets de la Loterie nationale de l’avenue de Wagram permet de découvrir à peu près toutes les relations géométriques et les nombres que l’on veut : le rapport entre la hauteur et la largeur de la fenêtre arrière est miraculeusement 3,142 (presque le nombre Pi), l’épaisseur de la tablette donne, aux unités près bien entendu, le même nombre que celui de la distance de la Terre au Soleil (voir encadré : « La Grande Pyramide : nombre d’or ou nombre 5 ? »). La date de la bataille de Poitiers et la formule chimique de la naphtaline ont également été retrouvées. Et si la pyramide de Kheops a une pente de 14/11, de nombreuses autres pyramides utilisent un autre rapport (6/5 pour la pyramide rouge, 4/3 pour la pyramide de Khephren ou encore 7/5 pour la pyramide rhomboïdale). C’est donc à un autre calcul qu’il faut s’atteler pour trouver le nombre d’or dans ces constructions. Mais la tâche ne semble pas impossible.
Pour faire entrer la face avant du Parthénon dans un rectangle d’or, il faut, soit ne pas complètement s’ajuster au toit, soit ne considérer que trois des quatre marches du socle.

Si quelqu’un s’amusait à relever les proportions du Washington Monument (dans la capitale fédérale) telles qu’elles sont indiquées dans le World Almanac, il y discernerait une quintuplité non moins remarquable. Ce monument mesure 555 pieds 5 pouces de haut, 55 pieds carrés à la base ; ses fenêtres s’ouvrent à 500 pieds du sol ; le produit de la base par 60 (soit 5 fois le nombre de mois dans l’année) donne 3 300 soit le poids exact de la pierre de faîte en livres anglaises. De plus, le mot Washington se compose exactement de dix lettres (deux fois cinq). Et si l’on multiplie la base par le poids de la pierre de faîte, on a 181 500, une approximation très poussée de la vitesse de la lumière en miles par secondes. Si on prend pour unité le « pied monumental », légèrement plus court que le pied étalon, la base mesurera 56 pieds 1/2 de côté. Ce chiffre, multiplié par 33 000, donne cette fois un résultat plus approché encore de la vitesse de la lumière.
N’est-il pas significatif aussi que le monument affecte la forme d’un obélisque ? Ou encore, que sur le billet d’un dollar, la grande pyramide apparaisse au verso d’un portrait de Washington ? Bien mieux, la décision d’imprimer la pyramide (c’est-à-dire le revers du sceau des États Unis) sur les dollars fut annoncée par le secrétaire d’État au Trésor le 15 juin 1935, jour et année multiples de 5 tous les deux. Et ne trouve-t-on pas vingt-cinq lettres exactement (cinq fois cinq) dans le titre The Secretary of the Treasury ? Il faudrait environ cinquante-cinq minutes à un mathématicien moyen pour découvrir toutes ces « vérités », en travaillant uniquement sur les maigres données fournies par l’Almanach. Si l’on considère que Smyth [Charles Piazzi Smyth, 1819, 1900, astronome royal d’Écosse, qui prétendit avoir trouvé des vérités fondamentales dans les dimensions de la grande pyramide, et dont les ouvrages eurent un succès retentissant] effectuait lui-même ses relevés, récoltant ainsi des centaines de mesures, et qu’il passa une vingtaine d’années à ruminer là-dessus, on conçoit sans peine qu’il ait pu parvenir à des résultats aussi extraordinaires.
Néanmoins, les ouvrages de Smyth firent une forte impression sur des millions de lecteurs naïfs. On vit paraître des dizaines de volumes, dans toutes les langues, apportant chacun leur caillou à la grande œuvre. En France, la pyramidologie eut pour chef de file l’abbé F. Moigno, chanoine de Saint-Denis. Un « Institut International pour la Conservation et le Perfectionnement des Poids et Mesures » fut fondé à Boston en 1879, au cours d’une assemblée tenue à l’Old South Church. Cette société se donnait pour but la révision des unités de mesure, conformément aux étalons sacrés de la pyramide, et la lutte contre le « système métrique athée » de la France.

Pour retrouver le rectangle d’or, il faut opérer quelques choix de cadrage bien arbitraires : une partie du bras oublié, vêtements, etc.).
Des constructions tout aussi arbitraires sont nécessaires pour retrouver a posteriori le nombre d’or dans les tableaux de Léonard de Vinci (voir le tableau représentant Saint-Jérôme).
Le célèbre croquis « L’homme de Vitruve », supposé illustrer de façon emblématique le rôle du nombre d’or dans les proportions du corps humain, est basé en réalité sur un cercle, un carré et des divisions en quarts et en huitièmes. Léonard de Vinci ne mentionne pas cette proportion lorsqu’il traite de la composition du corps humain.
Une présence parfois bien réelle, mais pas mystérieuse
Si donc la reconstruction a posteriori d’une conception à base du nombre d’or semble bien arbitraire (et pas très difficile), il existe des cas, en peinture ou en architecture, où le nombre d’or est intentionnellement présent. Il en est ainsi de la Cité radieuse de Marseille, où Le Corbusier a explicitement utilisé le nombre d’or et la suite de Fibonacci (système de proportion Le Modulor, inventé par l’architecte). Les peintres Dali et Picasso l’ont également utilisé par jeu.
Lié à certaines formes géométriques (dodécaèdre ou icosaèdre) et à la suite de Fibonacci, il n’est alors pas surprenant de retrouver le nombre d’or dans la nature lorsque ces formes géométriques sont impliquées, ou lorsque la suite de Fibonacci est présente. Nulle considération d’« esthétique divine » n’est nécessaire. C’est ainsi le cas en phyllotaxie dans des structures spiralées (pomme de pin par exemple, voir encadré).
L’origine du mythe de l’esthétique du nombre d’or
La fascination pour le nombre d’or remonte à loin. Le moine franciscain Luca Pacioli lui consacre en 1509 un livre, De divina proportione. Les propriétés géométriques y sont étudiées, ainsi que ses relations avec certains polyèdres, dont le dodécaèdre qui représente l’univers chez Platon. Léonard de Vinci illustrera l’ouvrage avec 60 dessins de polyèdres. Ce travail témoigne d’abord d’un intérêt pour la géométrie, dans la lignée d’Euclide et des pythagoriciens. Mais Luca Pacioli semble être le premier à y avoir ajouté une référence à l’esthétique de cette proportion 7. Il faudra toutefois attendre le 19e siècle et l’œuvre d’un professeur de philosophie allemand, Adolf Zeising (1810-1876), pour voir la section dorée érigée en norme ou valeur esthétique. Mais c’est Matila Ghyka, prince et diplomate roumain, qui va véritablement lancer le mythe avec son ouvrage Le nombre d’or 8 (écrit en français). C’est à lui que l’on doit une revisite détaillée de l’art et de l’architecture, et la « découverte » du nombre d’or dans les cathédrales, les temples grecs ou les tableaux de grands peintres.
Il existe plusieurs types de dispositions des feuilles le long d’une tige. Pour les plantes verticillées, les feuilles apparaissent en même temps au même endroit de la tige. Pour les plantes dites spiralées, les feuilles apparaissent une à une le long de la tige en formant des spirales. Ce qu’il est surprenant de constater, c’est que pour les plantes spiralées, l’arrangement est directement lié à la suite de Fibonacci, et donc au nombre d’or.
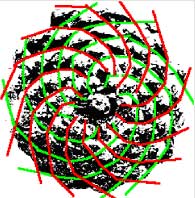
Marque divine ? Inscription du nombre d’or dans le code génétique ? Plusieurs interprétations de ce genre ont bien entendu été proposées. L’explication a été apportée par les physiciens Stéphane Douady et Yves Couder qui ont réalisé un système physique à l’aide de gouttes d’un fluide ferromagnétique placé dans un champ magnétique. Les contraintes stériques (occupation de l’espace) de la naissance des massifs cellulaires responsables de la formation d’une feuille ont été reproduites, et la même organisation, liée à la suite de Fibonacci, a ainsi été reproduite en laboratoire. Des simulations numériques ont donné les mêmes résultats. Il s’agit donc bien d’une conséquence de contraintes d’encombrement et d’optimisation de l’espace disponible qui conduit à la répartition liée au nombre d’or, et non pas un code génétique.
Un mythe encore bien vivant…
Les ouvrages de démystification existent, et le doute n’est plus de mise. Pourtant, on trouve encore quelques sources sérieuses pour prêter crédit à ces belles fables. Par exemple, le site des Arts appliqués de l’Université de Nice 9 fait la part belle à toutes les légendes sur la « divine proportion ».
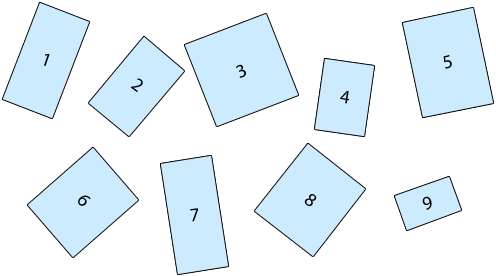
Les rectangles correspondant au nombre d’or sont les rectangles n° 2 et 9. Dans un sondage réalisé par deux étudiants auprès de 1178 de leurs collègues de l’École Polytechnique Fédérale de Lausanne, seuls 23 % des personnes interrogées ont identifié ces rectangles comme étant les mieux proportionnés à leurs yeux. Le rectangle n° 5 remporte à lui tout seul 35 % des suffrages, avec une proportion de 1,35, assez éloignée de la valeur du nombre d’or (1,618).
Des expériences de psychologie sont également invoquées. En particulier, celles réalisées en 1876 par le philosophe allemand Gustav Fechner. Des sujets, à qui l’on présente une série de 10 rectangles avec des rapports hauteur/largeur variant entre 1 (carré) et 0,4, sont invités à indiquer la figure qui leur paraît la plus esthétique. Les rapports les plus souvent retenus seraient ceux s’approchant de la « proportion dorée ». De là vient le mythe de la beauté naturelle du nombre d’or. De nombreux biais méthodologiques ont été soulevés à l’encontre de ces expériences. En 1992, George Markowsky a repris ces expériences 10 en utilisant différentes méthodes de présentation des rectangles, différentes séries de rectangles, etc. Le nombre d’or ne ressort plus spécialement, et la valeur retenue en majorité va varier d’une expérience à l’autre. On peut d’ailleurs se demander pourquoi, si ce rapport est particulièrement harmonieux et esthétique, il n’est pas utilisé par les peintres pour les dimensions d’encadrement des tableaux.
…aux relents frisant parfois le racisme
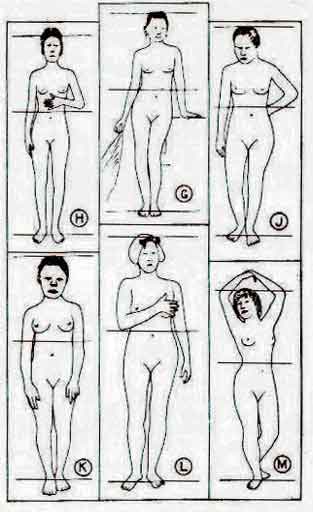
Dans un livre reprenant tous les clichés et tous les mythes pseudo-scientifiques d’un cerveau droit siège de l’intuition, et d’un cerveau gauche siège de l’analyse et de la logique, le médecin cancérologue Lucien Israël 11 se livre à un véritable plaidoyer de la supériorité de la « culture occidentale », ayant su mettre en œuvre une authentique pédagogie des deux cerveaux, et menacée d’effondrement, « au contact d’immigrés attirés par une vie plus facile [… qui] rêvent de nous soumettre à leur culture, sinon de réduire et d’altérer la nôtre » 12. Un chapitre consacré au nombre d’or nous apprend que notre cerveau est mystérieusement accordé à ce nombre, et que c’est pour cela que nous trouvons belles les figures basées sur ces proportions.
Don Neroman (1884-1953) va encore plus loin 13. Pour lui, l’homme idéal et bien proportionné est celui dont la hauteur du nombril ramené à la taille de l’individu respecte la « proportion divine ». Comparant divers clichés de femmes de « races les plus diverses » (voir figure), il affirme que certaines ont les jambes trop courtes par rapport au buste, signe propre « aux adolescents qui n’ont pas encore atteint leur taille définitive ». D’où cette conclusion sans appel : « s’il existe une race dont le nombril est trop bas pour la grande majorité des individus, cette race n’a pas encore atteint sa maturité ». Et cet écart « est surtout accusé chez la Juive (figure M) et chez la jeune négrille de l’Afrique équatoriale (figure K). ».
Conclusion
Le nombre d’or possède, comme beaucoup de nombres, des propriétés fascinantes (géométrie, suite de Fibonacci, etc.) qui le font se retrouver dans de multiples domaines de la nature (le nombre Pi est probablement largement plus représenté). Mais il n’a pas de propriété esthétique particulière et n’a pas été utilisé par les architectes de l’Antiquité ou du Moyen Âge, ni par les grands peintres de la Renaissance. Il n’est pas spontanément reconnu par un être humain comme étant la proportion la plus harmonieuse. Et pour qui veut le retrouver dans une construction ou une figure, juste un peu de patience ou d’imagination suffisent. Bref, un mythe sans beaucoup de fondement…
À moins que… Regardez de plus près la revue que vous tenez en main… N’est-elle pas harmonieuse ? Munissez-vous d’un double décimètre et d’une petite calculette… Surprenant non ?
[(
1 | Misconceptions about the Golden Ratio, George Markowsky, The College Mathematics Journal, Vol. 23, No. 1, Jan. 1992, 2-19.
2 | « La numérologie du nombre d’or », Jean-Paul Delahaye, dans Les inattendus mathématiques (Éditions Belin – Pour la science 2004).
3 | Le nombre d’or, Marguerite Neveux et H. E Huntley (Poche – 24 octobre 1995)
1 À ne pas confondre avec le nombre d’or utilisé en astronomie. On attribue à l’astronome grec Méton la découverte un peu avant 400 av. J.-C. que 19 années solaires valent 235 lunaisons. Découverte essentielle permettant de fixer le calendrier. Les Athéniens ont fait graver ce cycle en lettres d’or sur un temple de la cité.
2 Voir par exemple : http://www.solest.com/opinion/239.htm (disponible sur archive.org—17 sept. 2019).
3 Voir « le nombre d’or et les arts » sur http://www.crdp-montpellier.fr/prod....
4 Voir par exemple Le fascinant nombre Pi, Jean-Paul Delahaye, Belin Pour la science, 1997.
6 Jean-Pierre Adam, Le passé recomposé : chronique d’archéologie fantasque, éditions du Seuil, 1998, cité par Jean-Paul Delahaye. Martin Gardner a procédé de même avec Washington Monument, obélisque en l’honneur du premier président américain (Fads and Falacies in the name of science, 1957). Voir l’encadré.
8 Le nombre d’or, Gallimard, 1931, réédité en 1959.
9 http://www.ac-nice.fr/artsap/fichedocumen/nombredor.html (disponible sur archive.org—17 sept. 2019).
11 Cerveau droit, cerveau gauche, cultures et civilisations, Plon, 1995.
12 Ibid, page 290.
13 Don Neroman, Le nombre d’or, clé du monde vivant.
Publié dans le n° 278 de la revue
Partager cet article
L' auteur

Jean-Paul Krivine
Rédacteur en chef de la revue Science et pseudo-sciences (depuis 2001). Président de l’Afis en 2019 et 2020. (…)
Plus d'informationsNumérologie et nombre d’or
Le mythe du nombre d’or
Le 30 novembre 2007
Des nombres fétiches pour gagner (plus) au loto
Le 2 décembre 2007
Mieux que le hasard !
Le 29 novembre 2007
Sous le signe du 7
Le 24 novembre 2007
La numérologie dans les entreprises
Le 24 novembre 2007