Journaux prédateurs
Les simplificateurs de pi
Publié en ligne le 26 décembre 2016 - Vulgarisation scientifique -Le nombre π (le périmètre d’un cercle de diamètre 1) peut se calculer de mille façons différentes par des formules de toutes sortes : limites de suites particulières (qui par exemple convergent vers la longueur du périmètre d’un cercle de diamètre 1 ; c’est l’idée de la méthode d’Archimède), intégrales (donnant par exemple l’aire d’un disque de rayon 1), séries infinies, produits infinis, etc. Toutes ces formules et méthodes conduisent au même résultat, ce que l’on démontre. On peut aussi le constater en calculant dans chaque cas 10, 100, 1 000 ou beaucoup plus de décimales et en comparant. Personne ne peut douter aujourd’hui que :
Cependant, π reste compliqué, et l’être humain, qui – avec raison – cherche à simplifier tout ce qui peut l’être, rêve de formules plus simples que toutes celles connues.
Dans la Bible [1], de manière indirecte on trouve la valeur π = 3. C’est une belle simplification, mais il ne s’agit pas d’un texte mathématique et il n’est pas certain que le passage qu’on interprète de cette façon signifiait vraiment pour ses auteurs que π = 3.
Un authentique simplificateur de π est Edward Johnson Goodwin qui a presque réussi à faire adopter une loi pour imposer ses « découvertes ». En 1897, il mena une série de raisonnements et de calculs dont l’un donnait π = 3,2 = 16/5. Il proposa à l’État d’Indiana d’en faire une constante officielle pour simplifier la vie de tous. L’intention était louable. Heureusement, il échoua [2].
Un peu après la parution de mon livre sur π [3], en 1997, j’ai reçu une dizaine de lettres d’un mathématicien amateur du midi de la France qui me proposait une valeur de π assez simple :
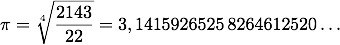

Je tentais en vain de le ramener à la raison : son expression faisait de π un nombre algébrique (solution d’une équation polynomiale à coefficients entiers), alors qu’on a démontré, il y a plus d’un siècle, que π est transcendant – donc n’est pas algébrique [4]. La formule de mon correspondant donnait aussi une solution au problème de la quadrature du cercle, qui n’en a pas 1. Ce qui m’avait frappé était la conviction très forte de l’auteur, la confusion de ses arguments, et son hostilité à l’égard de l’autre π (celui de tout le monde) qu’il appelait avec insistance et hargne « l’usurpateur ». Ce simplificateur de π , à ma connaissance, ne parvint jamais à publier ses élucubrations qui sont donc restées dans ses dossiers et les miens.
Tout est publiable
Les temps ont changé et, grâce à Internet et à la multiplication récente de pseudo-journaux scientifiques, toute idée, aussi farfelue soit-elle, peut aujourd’hui trouver sa place sur le réseau et même comme article dans une revue prétendument scientifique. Toute folie est en mesure de se déclarer « validée par la communauté académique », ce qui trompera les journalistes peu attentifs et les amateurs mal informés, et parfois même certains scientifiques ignorants de cette évolution.
J’ai pris conscience de cette nouvelle situation en recevant il y a quelques mois un livre (en version pdf) que m’a fait parvenir son auteur. Jamais un simplificateur de π n’avait aussi bien réussi que ce Sarva Jagannadha Reddy qui se présente comme un Retired Zoology Lecturer habitant 19-42-S7-374, S.T.V. Nagar, Tirupati, 517 501, India.
Son livre écrit en anglais est intitulé The Gayatri π value [5]. Que l’on puisse publier n’importe quoi n’est pas une nouveauté : lui-même avait auparavant publié des livres sur Internet donnant sa version simplifiée de π. Et bien d’autres avant lui ont publié à compte d’auteur des solutions du problème de la quadrature du cercle. Ce qui m’a étonné est que le livre reçu est composé de la reproduction de quinze articles dont la plupart avaient auparavant été publiés dans des revues scientifiques d’apparence académiques : IOSR (International Organization of Scientific Research), Journal of Mathematics, International Journal of Mathematics and Statistics Invention, Internatio-nal Journal of Engineering Inventions, International Journal of Latest Trends in Engineering and Technology, IOSR Journal of Engineering.
Je n’en connaissais aucune, mais toutes, au moment de la publication, appartenaient à la catégorie des nombreuses revues récentes où l’auteur paie pour être publié et où le contrôle scientifique par une expertise demandée à des personnalités compétentes est léger, simulé, ou même totalement inexistant. Ces fausses revues (parfois appelées journaux prédateurs ou fake journals en anglais) sont une plaie pour la communauté scientifique et l’exemple de Sarva Jagannadha Reddy en est une démonstration claire et sans appel. Une liste des éditeurs de ces journaux est maintenue à jour [6]. Pour toute revue sérieuse confrontée aux affirmations de Sarva Jagannadha Reddy, ou bien ce que prétend l’auteur est vrai et c’est une révolution méritant la une de tous les journaux (je dis bien tous les journaux, Le Monde, le Wall Street Journal, etc.) car c’est la totalité des mathématiques qui serait par terre ; ou bien c’est faux et elle se déshonore en publiant une bêtise aussi énorme.
Les articles reproduits dans le livre reçu proposent tous des arguments, bien sûr ridicules et sans aucune valeur réelle, prouvant que π = (14 – √2)/4, soit approximativement 3,1464466094... Comme pour mon correspondant du sud de la France, la formule fait de π un nombre algébrique, ce qui, s’ils avaient raison, serait une révolution mathématique sans précédent contredisant un résultat (la transcendance de π) démontré par de nombreuses méthodes différentes et dont pas un mathématicien ne doute…
Pour l’auteur, la valeur de π admise par le reste du monde provient d’erreurs de raisonnements qu’il analyse, montrant qu’il n’a vraiment rien compris même à ce que le grand Archimède avait déjà correctement perçu il y a 2000 ans, et qui depuis est devenu plus précis encore quand le concept de nombre réel a été mieux maîtrisé. Je ne discuterai pas ici des erreurs de Sarva Jagannadha Reddy, d’autres l’ont fait et en ont précisément identifié certaines [7].
Simplifier π est un rêve et c’était sous une forme géométrique celui de tous les quadrateurs du cercle. Le fait que le nombre π soit transcendant est la preuve qu’il ne pourra jamais se simplifier beaucoup et que les amateurs qui veulent s’affranchir de la réalité du monde complexe des mathématiques perdent leur temps.

Une littérature prétendument scientifique
Il est quand même navrant que se soit développée une littérature, prétendument scientifique, prête à tout pourvu qu’on paie. Elle nuit au bon fonctionnement de la science. Cette littérature donne l’illusion à certains de mener un travail contrôlé et reconnu, ce qui n’est pas vrai. Cela rend plus difficile à l’amateur sincère et curieux de faire le tri entre la science et le simulacre de la science. Le mode de fonctionnement libéral de notre économie qui autorise tout le monde à créer son propre journal, les possibilités offertes par Internet d’introduire des pseudo-revues par centaines sans contrôle et presque sans coût, et l’appât du gain de quelques escrocs sans scrupules qui mettent en place ces revues et inondent le monde de courriels pour les faire connaître et attraper les clients naïfs, voilà les causes de ce nouvel état du monde où les simplificateurs de π : peuvent faire semblant de découvrir des vérités qui n’en sont pas, et se présenter comme les ayant publiées et fait reconnaître par le monde savant.
1 | Steven Dutch, “π in the Bible ?”, 1998. (disponible sur archive.org—9 juin 2020)
2 | Indiana π Bill, sur Wikipedia en anglais.
3 | Jean-Paul Delahaye, Le fascinant nombre π, Éditions Belin, 1997
4 | www.pi314.net/sitepdf/lindemann.PDF
5 | Reddivari Sarva Jagannadha Reddy, “New Method of Computing π”
6 | Scholarly Open Access : “Critical analysis of scholarly open-access publishing” www.scholarlyoa.net
7 | www.acmescience.com/2012/07/spot-the-error/
Pour aller plus loin :
- Lukić Tin et al., “Predatory and Fake Scientific Journals/Publishers – A Global Outbreak with Rising Trend : A Review”, Geographica Pannonica, Volume 18, Issue 3, 69-81, septembre 2014. Un article de fond sur le sujet.
- “Unreliable research : Trouble at the lab”, The Economist, 19 octobre 2013. Sur economist.com. Un article de fond sur le contrôle de ce qui est publié.
- John Bohannon, “Who’s Afraid of Peer Review ?”, Science, 4 Oct 2013, sur science.sciencemag.org. Un article sur le manque de sérieux de certaines publications.
« Un maïs OGM reconnu toxique pour l’alimentation animale » (L’Humanité, 27 janvier 2016), « Une nouvelle étude du professeur Séralini démontre la toxicité d’un OGM sur des vaches » (Reporterre, 23 février 2016). Michèle Rivasi, députée européenne Europe Écologie, « s’appuyant sur l’étude du professeur Gilles-Éric Séralini qui a observé en conditions réelles l’impact de l’ingestion de maïs Bt176 par des vaches sur une période de trois ans », n’écarte pas « l’idée d’un scandale sous-jacent avec les OGM », ajoutant « Des vaches sont mortes, d’autres ont eu de graves problèmes de santé... » (rapporté par La Provence, 19 février 2016). Mais sur quoi s’appuient ces annonces ? Sur un simple article co-signé par Gilles-Éric Séralini [1] publié dans une revue intitulée Scholarly Journal of Agricultural Science.
Un journal douteux. Les résultats rapportés par un article isolé, faut-il le rappeler, se doivent d’être examinés et confirmés par la communauté scientifique. Mais dans ce cas particulier, la méfiance la plus grande s’imposait. Une simple visite sur le site de la revue jette un premier trouble : l’onglet « Our policies » devant décrire la politique éditoriale renvoie sur une « erreur 404 » (page inexistante). De même pour « Our team », supposé donner la composition de l’équipe éditoriale (pages re-consultées le 30 août 2016). Le site scholarlyoa.com classe l’éditeur dans la liste des éditeurs de « journaux prédateurs », sortes de « fausses revues » où les auteurs paient pour être publiés et où le contrôle scientifique est pratiquement absent. Bizarrement, l’article de Séralini n’est resté en ligne qu’une journée, le nom de domaine du site du journal, basé au Nigéria, n’avait pas été renouvelé. Il est depuis réapparu.
Un contenu surprenant. L’article commence par une phrase qui aurait dû encore davantage modérer l’ardeur de n’importe quel journaliste ou observateur : « l’étude n’a pas été conçue comme une expérience scientifique ; il s’agit d’une observation détaillée d’une ferme laitière gérée classiquement avec des technologies avancées ». En résumé, l’article affirme que les vaches de l’exploitation sont tombées malades après avoir commencé à ingérer du maïs Bt176 et recommande des tests à plus long terme sur les animaux nourris au maïs génétiquement modifié. À côté de cette publication principale, un texte plus court raconte les démêlés juridiques du co-auteur et propriétaire de la ferme (Glöckner) contre Syngenta, distributeur du maïs incriminé (procès perdu par le fermier). Cette description est suivie de la narration des mésaventures du fermier où il est suggéré que Syngenta aurait poussé la femme du fermier à divorcer en inventant des violences conjugales. Finalement, l’agriculteur sera condamné à deux ans de prison pour le viol de sa femme et aura sa part de la vente de la ferme confisquée par la cour. Les nombreuses études scientifiques qui ont été faites concernant la toxicité des maïs Bt, y compris le Bt167 de Syngenta, sont passées sous silence. Par exemple, cette étude de 2008 sur trois ans de nourrissage de 53 moutons et leurs petits [2]. Également oublié le fait qu’un nombre incalculable d’animaux de ferme mangent des OGM Bt depuis presque vingt ans, sans problème, excepté semble-t-il, il y a quinze ans, pour douze vaches de la ferme Glöckner.
L’article ne relate donc pas une étude, même mal conduite, mais consiste en un simple témoignage rétrospectif. Pour une analyse plus détaillée de cette publication, voir par exemple [3].
Les journaux prédateurs ne servent pas que leurs éditeurs. En conclusion, cette histoire illustre l’usage qui peut être fait des journaux prédateurs. Outre la conférence de presse et un communiqué du CRIIGEN (association militant contre les OGM et s’autoproclamant comme « expertise indépendante »), l’affaire donnera lieu à une question écrite au Parlement européen [4]. L’écho médiatique a toutefois été, ici, relativement plus limité que pour d’autres affaires similaires. Mais la propension à ériger une étude isolée comme prouvant des résultats définitifs, particulièrement s’ils vont à l’encontre du consensus établi, est malheureusement trop répandu. Le phénomène s’en trouve aggravé par la facilité à trouver une revue prête à publier n’importe quoi ou presque, contre rémunération.
1 | Gottfried Glöckner et Gilles-Éric Séralini, “Pathology reports on the first cows fed with Bt176 maize (1997–2002)”, Scholarly Journal of Agricultural Science 6(1):1-8, January 2016.
2 | Massimo Trabalza-Marinucci et al. “A three-year longitudinal study on the effects of a diet containing genetically modified Bt176 maize on the health status and performance of sheep”, Livestock Science 113(2):178-190, February 2008.
3 | « Les vaches de Gottfried Glöckner ressuscitées par Gilles-Éric Séralini et les “Verts”... pour 24 heures », sur seppi.over-blog.com
4 | www.europarl.europa.eu/sides/getDoc...
1 Le problème de la quadrature du cercle, énoncé dès l’Antiquité, consiste à construire un carré de même aire qu’un disque donné avec la seule aide d’une règle et d’un compas. Ce n’est qu’en 1882 que le mathématicien allemand Ferdinand von Lindemann démontra l’impossibilité de le résoudre de façon exacte. Cette démonstration repose sur le fait que π n’est pas un nombre algébrique.
Thème : Vulgarisation scientifique
Mots-clés : Mathématiques - Science
Publié dans le n° 318 de la revue
Partager cet article
L' auteur

Jean-Paul Delahaye
est professeur émérite à l’université de Lille et chercheur au Centre de recherche en informatique signal et (...)
Plus d'informationsVulgarisation scientifique

L’épigénétique
Le 22 janvier 2024
La renaissance des dinosaures
Le 14 juin 2022
Quand l’épigénétique s’en mêle
Le 11 mars 2022
Envisager la mathématisation du quotidien
Le 29 juillet 2020