Probabilités subjectives
Publié en ligne le 15 avril 2009 - Statistiques et probabilité -En prenant le train pour me rendre à Nancy, je me suis trouvé placé à côté d’un brave homme avide de discussion. Nous nous mettons à bavarder, de si bonne humeur que les passagers nous lancent des regards réprobateurs. En nous racontant nos vies, nous découvrons finalement que nous avons un ami commun : Pierre. « Que le monde est petit ! » nous exclamons-nous de concert, et nous comprenons tous les deux que la vie a quelque chose de magique, faisant se rencontrer contre toute attente des voyageurs partageant une même accointance. Je sais bien que la théorie mathématique des graphes, avec ses « small worlds », a réussi à montrer qu’un tel événement, la rencontre fortuite d’un ami d’ami, n’est en rien improbable. Malgré tout, je suis étonné par cette coïncidence mystérieuse…
Dans la même veine mais plus généralement, un résultat de la psychologie, depuis longtemps établi et abondamment démontré, est que l’être humain n’est pas rigoureux avec les probabilités intuitives (« subjectives » disent les psychologues), ne comprend pas le hasard précisément. Et parce que nous ne percevons pas le hasard tel qu’il est, nous sommes interloqués par des phénomènes que le hasard véhicule tout naturellement, et impassibles face à d’autres que la théorie des probabilités montrent invraisemblables. De nombreuses illusions, de nombreux « biais » déforment ainsi notre perception du hasard, et nous poussent à croire les allégations des pseudo-sciences, à accorder foi à certaines superstitions. Tels sont le biais d’équiprobabilité et l’attente excessive d’étalement.
Biais d’équiprobabilité
Le succès de l’astrologie tient entre autres choses au fameux effet Barnum, qui nous fait adhérer à toute description de notre personnalité un tant soit peu flatteuse. Mais l’astrologie ne se cantonne pas à la description des traits de personnalité. Elle prédit l’avenir, vous informe sur ce qui va vous arriver la semaine prochaine. Et les prédictions se réalisent plus d’une fois sur deux, ce qui est bien la preuve de l’efficacité de l’astrologie.
Prenant le parti de la science, je décidai récemment de tester rigoureusement mes horoscopes. Il y a trois semaines, il prédisait des problèmes de santé dans ma famille, et ma fille est tombée malade : une méchante grippe. Pas plus tard que la semaine dernière, on m’avait prédit une bonne nouvelle, et un article important (pour moi, pas pour l’humanité) a été accepté. Depuis des mois, le taux de succès de l’astrologie avoisine les 90 %. Neuf fois sur 10, ce que disent les étoiles se réalise ! On est bien loin d’un maigre 50 % de prévisions justes, que devrait, normalement, apporter une méthode aléatoire.
J’en étais là de mes réflexions lorsque je m’aperçus avec stupeur que depuis plusieurs mois je m’étais régulièrement trompé de ligne, lisant les prévisions des taureaux alors que je suis balance. Vous imaginez mon incrédulité. M’aurait-on menti sur ma date de naissance ? Non : vérification faite, les prévisions pour les balances sont tout aussi fiables, quoique fort différentes.
Comment expliquer ce paradoxe ? L’une des explications possibles est que j’ai une tendance naturelle à reconnaître dans une expression floue (« une période difficile » par exemple) ce qui m’arrive réellement. Mais on peut aussi dire – les deux explications sont tout à fait compatibles – que je suis tombé dans le biais d’équiprobabilité. J’ai supposé sans m’en rendre compte que si l’astrologie n’a rien à dire de spécial, alors elle doit voir juste une fois sur deux. C’est que l’homme a du hasard une définition intenable selon laquelle tout processus aléatoire est par essence équiprobable 1 : ainsi, une pièce truquée n’est pas pour nous une vraie machine aléatoire. Et pourtant, le hasard n’est pas toujours équiprobable, et si je prédis à un quidam qu’il ressentira, dans la semaine qui suit, un état d’énervement suscité par des membres de sa famille mais finira par penser qu’il aime tout de même ses proches, bien que ma prédiction ne repose sur rien, j’ai une grande probabilité de tomber juste.
Cette conviction que toute prédiction aléatoire doit tomber juste une fois sur deux seulement est l’une des déformations systématiques de notre perception du hasard, et elle nous fait trouver miraculeux ce qui est probable : la réalisation des prédictions horoscopiques. Je me demande ce que donnerait par exemple le test d’un sourcier à qui on demanderait, en Normandie où il professe, de déterminer par sa science un endroit où l’on pourra creuser sans trouver d’eau…
Attente excessive d’étalement
Des psychologues ont remarqué depuis longtemps que lorsque nous essayons d’inventer des séries de « pile ou face » conformes à ce que donnerait une pièce non truquée, nous avons une tendance générale à alterner les P (pile) et F (face). On préfèrera par exemple PFP à PPP. Le premier, qui alterne les P et les F, nous semble plus aléatoire.
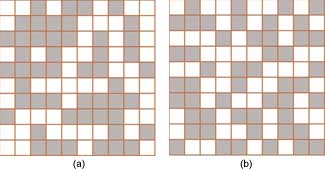
En généralisant ce fait à des situations géométriques, les psychologues Falk et Konold ont découvert que nous avions de même tendance, lorsque nous plaçons par exemple des pions sur un damier « au hasard » à les écarter les uns des autres de manière excessive, en évitant de laisser deux ou trois pions contigus. Et lorsque nous observons des placements de pions sur un damier, les répartitions réellement aléatoires nous semblent trop peu étalées, alors que les distributions artificiellement dispersées (mais pas trop) nous satisfont pleinement, et nous croyons y reconnaître du hasard authentique.
Cette illusion persistante explique par exemple la genèse de l’adage superstitieux : « Jamais deux sans trois », né du fait que nous croyons constater que les malheurs arrivent par groupe, en séries, en tout cas plus resserrés que ce que donnerait – pensons-nous – un tirage aléatoire. Si nous tirons, pour faire simple, douze dates au hasard dans l’année, l’homo sapiens moyen s’attendra à trouver à peu près une date par mois (et non trois en janvier). On ne serait même pas surpris de trouver exactement une date par mois, chose qui pourtant a une probabilité extrêmement faible de se produire, puisque cette chance est de 0,005 % 2... La probabilité que deux dates tombent la même semaine est de 26 % : il n’y aurait donc rien d’étonnant à cela, mais c’est pourtant un résultat qui nous laisserait pantois.
Ce qui nous semble d’incroyables coïncidences – une suite de désastres rapprochés dans le temps, le fait qu’on rêve de quelqu’un que l’on croise le lendemain – ne sont bien souvent que des banalités probabilistes. Mais les calculs permettant de déterminer si l’événement devrait être considéré comme étonnant ou non sont assez complexes pour le profane, qui se rabat du coup sur une estimation intuitive, une probabilité subjective, souvent très éloignée de la vérité.
La bonne probabilité ?
Ce que montrent le biais d’équiprobabilité et l’attente excessive d’étalement est, de manière assez générale, que nos estimations intuitives sont bien souvent en décalage total avec ce que dit la science du hasard. Mais il y a pire, ou du moins un autre biais qui s’ajoute à tout cela. Non seulement nous estimons mal les probabilités, mais nous ne cherchons pas toujours à estimer la bonne, parce que nous négligeons (ou ne connaissons pas) des informations indispensables.

Tous les médecins savent qu’il se produit régulièrement des guérisons inexpliquées. Un cancéreux se retrouve en pleine forme, un asthmatique n’a plus de crise d’un coup et pendant des années. Ces guérisons, parfois qualifiées de miraculeuses, ne sont pas surnaturelles. Elles sont seulement inexpliquées.
Le médecin ne sait pas ce qui détermine l’amélioration du patient (repos, changement de régime alimentaire), mais se réjouit pour lui.
Pourquoi alors serions-nous surpris d’apprendre qu’à Lourdes aussi, il arrive que certaines personnes se trouvent aller mieux ? Le contraire serait surprenant. Soyons honnêtes : ce n’est pas une guérison isolée qui émeut le public, mais la quantité de ces « miracles ». Plusieurs dizaines seraient avérés. Que pensons-nous alors spontanément ? Que s’il est déjà assez improbable qu’un malade se trouve subitement soulagé, il est encore bien plus étonnant que 60 ou 70 malades se trouvent guéris. Et le raisonnement semble imparable. On n’a jamais vu dans les couloirs des urgences 70 patients se relever d’un coup et partir en gambadant !
Las ! Le calcul intuitif que l’on fait laisse de côté une donnée de poids : le nombre de malades ayant mis les pieds à Lourdes. Il est certes étonnant que 70 malades désignés à l’avance se remettent sans soin, mais non pas que parmi des millions et des millions de malades qui se succèdent sans interruption depuis des lustres, 70 aient connu la rémission 3. C’est pourquoi, en admirateur modeste des probabilités, je n’attribue rien de surnaturel à ces guérisons, qui, à supposer qu’elles soient toutes réelles, ne représentent qu’une infime gouttelette dans l’océan des pèlerins. Et j’aimerais connaître – malsaine curiosité ? – le nombre de personnes mortes à Lourdes pendant qu’elles y cherchaient le salut.
Conclusion
Ces exemples ne sont que quelques-unes des déformations que notre cerveau imparfait nous inflige à propos du hasard. Mais à elles seules, les trois erreurs que nous avons citées expliquent pourquoi l’on peut voir dans le monde des miracles. Je dis voir car, à l’instar des illusions d’optique, ces illusions de notre perception du hasard ont la force de l’évidence, et ne plient pas facilement devant la raison. J’ai beau savoir que, dans l’expérience de Falk et Konold, le (a) est vraiment aléatoire, j’ai un œil en moi qui me montre la dispersion (b) et me susurre : voilà le vrai hasard !
1 | Falk, R. (1981). « The perception of randomness ». Proceedings of the fifth international conference for the psychology of mathematics education, 1, 222-229. Grenoble, France : Laboratoire IMAG.
2 | Gauvrit, N. (2009). Vous avez dit hasard ? Entre mathématique et psychologie. Paris : Belin/Pour la Science.
1 C’est-à-dire que chacun des événements possibles à la même probabilité d’apparition.
2 12!/1212 soit environ 0,005 %, ou 5 pour 100 000
3 Si la jambe d’un amputé repoussait, cela serait un miracle, même si l’événement est unique. Cependant, ce type de guérison ne se produit jamais. Comme le dit Jean Bricmont : « Dieu n’aime pas les amputés ».
Publié dans le n° 284 de la revue
Partager cet article
L' auteur

Nicolas Gauvrit
Chercheur en sciences cognitives au laboratoire Cognitions humaine et artificielle (CHArt) de l’École pratique des (…)
Plus d'informationsStatistiques et probabilité

À la louche, c’est louche
Le 30 décembre 2022
Nombres fétiches et statistiques pour gagner au Loto ?
Le 14 novembre 2022
Être né quelque part, c’est toujours un hasard
Le 28 janvier 2022![[Paris - 26 novembre 2019] Le hasard dans l'évolution de la vie](local/cache-gd2/53/27b1e9f51822ba92c9f78a1d480c82.jpg?1675292537)